Vraag 4
In figuur 2 kunnen we zien dat hoek α bepaald wordt door de verhouding tussen de krachten Flift en Fw,lucht. Als de Cessna horizontaal vliegt geldt dat de liftkracht gelijk is aan de zwaartekracht op het vliegtuig. Er geldt dusFlift = FZ = 9,81 · 710 kg = 6965,1 N
Fw,lucht kunnen we bepalen aan de hand van het vermogen van de motor. In de vraag staat dat het geleverde vermogen 70% van het topvermogen (100 pk) is. In BINAS tabel 5 vinden we de omrekenfactor van paardekracht naar Watt. Omrekenen geeft een vermogen van
P = 70% · 7,457·102 · 100 = 52199 W
Voor bewegend voorwerp met een constante snelheid geldt voor het vermogen dat nodig voor de beweging (zie BINAS tabel 35-A4)
P = F·v
Voor de kracht volgt hieruit
F = P/v = 52199 / 55 = 949,073 N
Dit is de kracht die de motor levert. Omdat alle krachten in evenwicht zijn weten we dat ook de luchtwrijving Fw,lucht gelijk is aan 949,073 N.
In figuur 2 zien we dat vanuit hoek α Fw,lucht de overstaande zijde is en Flift de aanliggende zijde. Er geldt dus
tan α = Fw,lucht / Flift
Voor α vinden we dan
α = tan-1 (949,073/6965,1) = 7,759°
Afgerond is dit 7,8°.
Vraag over "Cessna"?
Hou mijn naam verborgen voor andere bezoekersEerder gestelde vragen | Cessna
Op dinsdag 2 apr 2024 om 17:26 is de volgende vraag gesteld
wat betekent bij vraag 8: dt in het antwoord Ek = Ek + Pnetto·dt
en waarom kan Ek hierin terug komen in zijn eigen formule
Erik van Munster reageerde op dinsdag 2 apr 2024 om 17:33
“dt” is in modellen altijd de grootte van het tijdstapje. In dit model is het 0,001 seconden.
Ek = Ek + Pnetto*dt is geen formule maar een modelregel. Het “=“ teken betekent dus niet “is gelijk aan” maar “wordt”. Eigenlijk staat er dus
“de nieuwe Ek” = “de oude Ek” + Pnetto*dt
wat betekent bij vraag 8: dt in het antwoord Ek = Ek + Pnetto·dt
en waarom kan Ek hierin terug komen in zijn eigen formule
Erik van Munster reageerde op dinsdag 2 apr 2024 om 17:33
“dt” is in modellen altijd de grootte van het tijdstapje. In dit model is het 0,001 seconden.
Ek = Ek + Pnetto*dt is geen formule maar een modelregel. Het “=“ teken betekent dus niet “is gelijk aan” maar “wordt”. Eigenlijk staat er dus
“de nieuwe Ek” = “de oude Ek” + Pnetto*dt
Op vrijdag 25 feb 2022 om 19:01 is de volgende vraag gesteld
Waarom telt bij vraag 6 alleen de oppervlakte van de voorvleugels en niet die van de horizontale achtervleugels?
Erik van Munster reageerde op vrijdag 25 feb 2022 om 19:18
Staat in de opgave dat het alleen om de voorvleugels gaat: te zien in figuur 2 en in de uitleg van de betekenis van A bij vraag 4.
Bij vliegtuigen dient de achterstaart als “stabilizer” en samen met de kleppen die er op zitten dient om de stand van het vliegtuig te kunnen regelen (meer naar boven of meer naar beneden gerichtte hoek). Voor de liftkracht zijn de voorvleugels.
Waarom telt bij vraag 6 alleen de oppervlakte van de voorvleugels en niet die van de horizontale achtervleugels?
Erik van Munster reageerde op vrijdag 25 feb 2022 om 19:18
Staat in de opgave dat het alleen om de voorvleugels gaat: te zien in figuur 2 en in de uitleg van de betekenis van A bij vraag 4.
Bij vliegtuigen dient de achterstaart als “stabilizer” en samen met de kleppen die er op zitten dient om de stand van het vliegtuig te kunnen regelen (meer naar boven of meer naar beneden gerichtte hoek). Voor de liftkracht zijn de voorvleugels.
Op donderdag 24 feb 2022 om 22:50 is de volgende vraag gesteld
Bij vraag 4. In Binas staan in tabel 5 twee eenheden paardenkracht. Nml. hp en CV. In de uitwerking wordt de hp variant gebruikt. Waarom niet de CV variant? Die laatste wordt meen ik gebruikt bij motorvermogens van auto's. 100 kW is dan 136 pk.
Erik van Munster reageerde op vrijdag 25 feb 2022 om 15:37
hp staat in de opgave erbij vandaar dat je die hier gebruikt. Verschil tussen de verschillende paardenkrachten is historisch en heeft te maken met definities die in verschillende landen net iets verschillend zijn. Hp is Engels en CV is Frans en er bestaat ook nog een Duitse paardenkracht.
Bij vraag 4. In Binas staan in tabel 5 twee eenheden paardenkracht. Nml. hp en CV. In de uitwerking wordt de hp variant gebruikt. Waarom niet de CV variant? Die laatste wordt meen ik gebruikt bij motorvermogens van auto's. 100 kW is dan 136 pk.
Erik van Munster reageerde op vrijdag 25 feb 2022 om 15:37
hp staat in de opgave erbij vandaar dat je die hier gebruikt. Verschil tussen de verschillende paardenkrachten is historisch en heeft te maken met definities die in verschillende landen net iets verschillend zijn. Hp is Engels en CV is Frans en er bestaat ook nog een Duitse paardenkracht.
Op zaterdag 11 apr 2020 om 21:17 is de volgende vraag gesteld
hallo,
bij vraag 5 zie ik niet in hoe u op de laatste stap komt, via de ene laatste stap.
eenheid Clift = (kg m s-2) / (kg m-3 m2] m2 s-2) voor mij idee in deze stap komen niet alle m weg te vallen, m2 gaan wel weg maar m-3 blijft staan dacht ik?
eenheid Clift = kg m s-2 / kg m s-2
Erik van Munster reageerde op zaterdag 11 apr 2020 om 22:46
Als je alleen naar de m kijkt en de rest even weg laat staat er
m / ( m-3 m2 m2 )
m / (m-3 m4)
m / m
En dus valt m boven en onder de deelstreep tegen elkaar weg.
hallo,
bij vraag 5 zie ik niet in hoe u op de laatste stap komt, via de ene laatste stap.
eenheid Clift = (kg m s-2) / (kg m-3 m2] m2 s-2) voor mij idee in deze stap komen niet alle m weg te vallen, m2 gaan wel weg maar m-3 blijft staan dacht ik?
eenheid Clift = kg m s-2 / kg m s-2
Erik van Munster reageerde op zaterdag 11 apr 2020 om 22:46
Als je alleen naar de m kijkt en de rest even weg laat staat er
m / ( m-3 m2 m2 )
m / (m-3 m4)
m / m
En dus valt m boven en onder de deelstreep tegen elkaar weg.
Op woensdag 3 apr 2019 om 16:00 is de volgende vraag gesteld
Hallo Erik, bij vraag a heb ik het iets anders berekend, maar ik snap eigenlijk niet waarom er op deze manier een ander antwoord uit komt:
Fm= F,wlucht dus toen ik die had uitgerekend heb ik Flucht uitgerekend Flucht= wortel(Fz^2 + Fwlucht^2)= 7029,5 (ik zie inderdaad dat dat niet had gehoeven, want met TOA kan je het al berekenen). Toen heb ik met CAS, A= Flift= Fzw en S=Flucht de hoek uitgerekent cos-1= 8,6
In principe zou er dan toch hetzelfde uit moeten komen?
Erik van Munster reageerde op woensdag 3 apr 2019 om 17:13
Zou ook met Pythagoras en daarna cosinus moeten kunnen hoor. Staat je rekenmachine wel goed ingesteld? Als je iets met sin cos of tan doet moet hij op DEGREES [DEG} staan.
Hallo Erik, bij vraag a heb ik het iets anders berekend, maar ik snap eigenlijk niet waarom er op deze manier een ander antwoord uit komt:
Fm= F,wlucht dus toen ik die had uitgerekend heb ik Flucht uitgerekend Flucht= wortel(Fz^2 + Fwlucht^2)= 7029,5 (ik zie inderdaad dat dat niet had gehoeven, want met TOA kan je het al berekenen). Toen heb ik met CAS, A= Flift= Fzw en S=Flucht de hoek uitgerekent cos-1= 8,6
In principe zou er dan toch hetzelfde uit moeten komen?
Erik van Munster reageerde op woensdag 3 apr 2019 om 17:13
Zou ook met Pythagoras en daarna cosinus moeten kunnen hoor. Staat je rekenmachine wel goed ingesteld? Als je iets met sin cos of tan doet moet hij op DEGREES [DEG} staan.
Mina Fadhil vroeg op maandag 21 mei 2018 om 23:54
goedenavond Erik,
Ik begrijp nog niet helemaal hoe U van stap 2 naar 3 bent overgegaan, kunt U misschien een nadere uitleg geven?
Erik van Munster reageerde op dinsdag 22 mei 2018 om 15:19
Bij stap 2 staat er
Flift / (½·ρ·Avleugel·v2) = ½·ρ·Avleugel·Clift·v2 / (½·ρ·Avleugel·v2)
Aan de rechterkant van het =teken staat een grote deelstreep met in teller als de noemer een heleboel factoren die hetzelfde zijn: Zowel boven de deelstreep als onder de deelstreep staan: ½, ρ, Avleugel en v2. Alle factoren die boven en onder de deelstreep staan kun je altijd tegen elkaar wegstrepen. Als je dit doet vallen al deze factoren weg en hou je aan de rechterkant alleen nog Clift over.
goedenavond Erik,
Ik begrijp nog niet helemaal hoe U van stap 2 naar 3 bent overgegaan, kunt U misschien een nadere uitleg geven?
Erik van Munster reageerde op dinsdag 22 mei 2018 om 15:19
Bij stap 2 staat er
Flift / (½·ρ·Avleugel·v2) = ½·ρ·Avleugel·Clift·v2 / (½·ρ·Avleugel·v2)
Aan de rechterkant van het =teken staat een grote deelstreep met in teller als de noemer een heleboel factoren die hetzelfde zijn: Zowel boven de deelstreep als onder de deelstreep staan: ½, ρ, Avleugel en v2. Alle factoren die boven en onder de deelstreep staan kun je altijd tegen elkaar wegstrepen. Als je dit doet vallen al deze factoren weg en hou je aan de rechterkant alleen nog Clift over.
Op maandag 21 mei 2018 om 20:48 is de volgende vraag gesteld
Hallo Erik,
Hoe schrijf je zo een formule zoals bij vraag 5 correct om.
Groeten,
Shant
Erik van Munster reageerde op maandag 21 mei 2018 om 21:29
De formule die in de opgave gegeven staat is
Flift = ½·ρ·Avleugel·Clift·v2
Je wilt uiteindelijk de formule voor Clift. Dat betekent dat je alles moet wegwerken wat nu "om Clift heen staat" in de formule. Dit kan door links en rechts te delen door (½·ρ·Avleugel·v2). Je krijgt dan
Flift / (½·ρ·Avleugel·v2) = ½·ρ·Avleugel·Clift·v2 / (½·ρ·Avleugel·v2)
Aan de rechterkant valt dan van alles boven en onder de deelstreep tegen elkaar weg en je houdt over
Flift / (½·ρ·Avleugel·v2) = Clift
Dus
Clift = Flift / (½·ρ·Avleugel·v2)
(Als je meer wilt oefenen met omschrijven van formules: Kijk bij "oefenen" hierboven. Opgave 20 uit het hoofdstuk Algem
Hallo Erik,
Hoe schrijf je zo een formule zoals bij vraag 5 correct om.
Groeten,
Shant
Erik van Munster reageerde op maandag 21 mei 2018 om 21:29
De formule die in de opgave gegeven staat is
Flift = ½·ρ·Avleugel·Clift·v2
Je wilt uiteindelijk de formule voor Clift. Dat betekent dat je alles moet wegwerken wat nu "om Clift heen staat" in de formule. Dit kan door links en rechts te delen door (½·ρ·Avleugel·v2). Je krijgt dan
Flift / (½·ρ·Avleugel·v2) = ½·ρ·Avleugel·Clift·v2 / (½·ρ·Avleugel·v2)
Aan de rechterkant valt dan van alles boven en onder de deelstreep tegen elkaar weg en je houdt over
Flift / (½·ρ·Avleugel·v2) = Clift
Dus
Clift = Flift / (½·ρ·Avleugel·v2)
(Als je meer wilt oefenen met omschrijven van formules: Kijk bij "oefenen" hierboven. Opgave 20 uit het hoofdstuk Algem
Op vrijdag 4 mei 2018 om 18:24 is de volgende vraag gesteld
Hoi Erik,
zou je ook de v berekenen uit de s-t diagram? Als ik dit doe kom ik niet op 25 m/s. Waarom kan dat nu niet?
Erik van Munster reageerde op vrijdag 4 mei 2018 om 19:05
In het algemeen kun je uit een s,t-diagram inderdaad de snelheid bepalen door het tekenen van een raaklijn maar hier hoef je v niet zelf te bepalen op deze manier. Hij is direct af te lezen uit het v,t-diagram wat ook in de vraag staat.
Hoi Erik,
zou je ook de v berekenen uit de s-t diagram? Als ik dit doe kom ik niet op 25 m/s. Waarom kan dat nu niet?
Erik van Munster reageerde op vrijdag 4 mei 2018 om 19:05
In het algemeen kun je uit een s,t-diagram inderdaad de snelheid bepalen door het tekenen van een raaklijn maar hier hoef je v niet zelf te bepalen op deze manier. Hij is direct af te lezen uit het v,t-diagram wat ook in de vraag staat.
Berber Zandstra vroeg op maandag 26 mrt 2018 om 20:35
Hallo Erik,
Waarom heeft het vliegtuig bij vraag 10 de wind mee? Ik dacht namelijk door het v - vwind dat de vwind steeds van de snelheid af ging en daarom tegen was. Anders zou je (dacht ik) toch v + vwind krijgen? Bedankt!
Erik van Munster reageerde op maandag 26 mrt 2018 om 20:55
Het gaat om de snelheid van het vliegtuig ten opzichte van de lucht. Uit de situatie zonder wind kun je afleiden dat de snelheid van het vliegtuig ten opzichte van de lucht 35 m/s moet zijn om op te stijgen. Als er tegenwind is van 10 m/s hoeft het vliegtuig maar met 25 m/s ten opzichte van de grond te gaan om een snelheid van 35 m/s ten opzichte van de lucht te krijgen.
Hallo Erik,
Waarom heeft het vliegtuig bij vraag 10 de wind mee? Ik dacht namelijk door het v - vwind dat de vwind steeds van de snelheid af ging en daarom tegen was. Anders zou je (dacht ik) toch v + vwind krijgen? Bedankt!
Erik van Munster reageerde op maandag 26 mrt 2018 om 20:55
Het gaat om de snelheid van het vliegtuig ten opzichte van de lucht. Uit de situatie zonder wind kun je afleiden dat de snelheid van het vliegtuig ten opzichte van de lucht 35 m/s moet zijn om op te stijgen. Als er tegenwind is van 10 m/s hoeft het vliegtuig maar met 25 m/s ten opzichte van de grond te gaan om een snelheid van 35 m/s ten opzichte van de lucht te krijgen.
Op maandag 26 mrt 2018 om 20:17 is de volgende vraag gesteld
Hallo Erik,
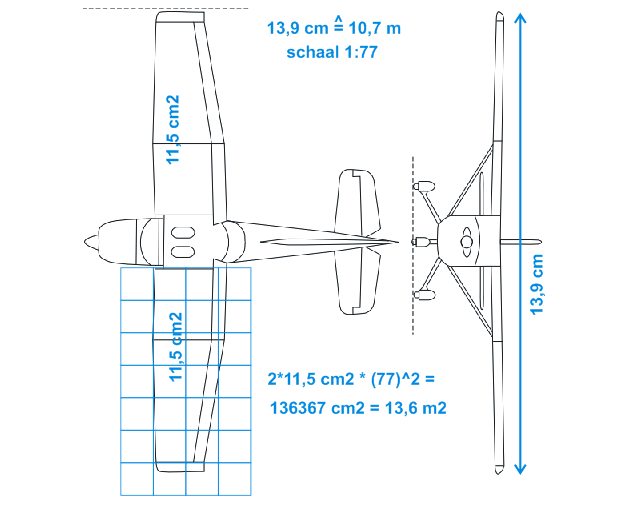
Bij vraag 5 zijn de getelde hokjes op 1 vleugel in totaal 11.5 cm^2. Ik tel echter ong. 12.5 cm^2. Weet jij hoe dit kan? En waarom doe je het aantal getelde hokjes keer 77^2 en niet alleen keer 77? Bedankt!
Op maandag 26 mrt 2018 om 20:18 is de volgende reactie gegeven
Sorry, ik bedoelde vraag 6.
Erik van Munster reageerde op maandag 26 mrt 2018 om 20:51
Hokjes tellen kan nooit met 100% precisie. Je mag er altijd een klein beetje naast zitten, ook op het eindexamen.
Het echte vliegtuig is in werkelijkheid 77 x zo groot. Één vierkant cm is dan dus in het echt een vierkant van 77 cm bij 77 cm. De oppervlakte hiervan is 77^2 = 5929 cm^2. Vandaar: het oppervlak is 77^2 keer zo groot.
Hallo Erik,
Bij vraag 5 zijn de getelde hokjes op 1 vleugel in totaal 11.5 cm^2. Ik tel echter ong. 12.5 cm^2. Weet jij hoe dit kan? En waarom doe je het aantal getelde hokjes keer 77^2 en niet alleen keer 77? Bedankt!
Op maandag 26 mrt 2018 om 20:18 is de volgende reactie gegeven
Sorry, ik bedoelde vraag 6.
Erik van Munster reageerde op maandag 26 mrt 2018 om 20:51
Hokjes tellen kan nooit met 100% precisie. Je mag er altijd een klein beetje naast zitten, ook op het eindexamen.
Het echte vliegtuig is in werkelijkheid 77 x zo groot. Één vierkant cm is dan dus in het echt een vierkant van 77 cm bij 77 cm. De oppervlakte hiervan is 77^2 = 5929 cm^2. Vandaar: het oppervlak is 77^2 keer zo groot.
Thomas Rous vroeg op vrijdag 23 mrt 2018 om 02:01
Beste Erik,
Hoe weet je bij vraag 10 dat het vliegtuig een snelheid heeft van 35m/s.
Ik hoor het graag!
Erik van Munster reageerde op vrijdag 23 mrt 2018 om 10:41
Het model stopt zodra Flift > Fz (regel 5). Dit is het moment dat het vliegtuig opstijgt. In het v,t-diagram kun je zien dat het model stop vlak voor t=20 s. De snelheid die je hier afleest is 35 m/s. Daaruit kun je concluderen dat het vliegtuig (zonder tegenwind) opstijgt bij v = 35 m/s.
Beste Erik,
Hoe weet je bij vraag 10 dat het vliegtuig een snelheid heeft van 35m/s.
Ik hoor het graag!
Erik van Munster reageerde op vrijdag 23 mrt 2018 om 10:41
Het model stopt zodra Flift > Fz (regel 5). Dit is het moment dat het vliegtuig opstijgt. In het v,t-diagram kun je zien dat het model stop vlak voor t=20 s. De snelheid die je hier afleest is 35 m/s. Daaruit kun je concluderen dat het vliegtuig (zonder tegenwind) opstijgt bij v = 35 m/s.